67 二叉树的典型遍历方式
二叉树的典型遍历方式
-
问题
二叉树是否只有一种遍历方式(层次遍历)?
-
典型的二叉树遍历方式
- 先序遍历(Pre-Order Traversal)
- 中序遍历(In-Order Traversal)
- 后序遍历(Post-Order Traversal)
-
先序遍历(Pre-Order Traversal)
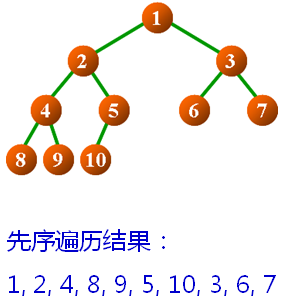
- 二叉树为空
- 无操作,直接返回
- 二叉树不为空
- 访问根结点中的数据元素
- 先序遍历左子树
- 先序遍历右子树
- 二叉树为空
-
先序遍历功能定义
preOderTraversal(node){
if(node!=nullptr){
access(node->value);
preOderTraversal(node->left);
preOderTraversal(node->right);
}
} -
中序遍历(In-Order Traversal)
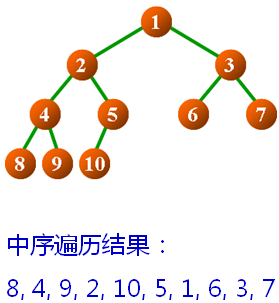
- 二叉树为空:
- 无操作,直接返回
- 二叉树不为空:
- 中序遍历左子树
- 访问根结点中的数据元素
- 中序遍历右子树
- 二叉树为空:
-
中序遍历功能定义
inOrderTraversal(node){
if(node!=nullptr){
inOrderTraversal(node->left);
access(node->value);
inOrderTraversal(node->right);
}
} -
后序遍历(Post-Order Traversal)
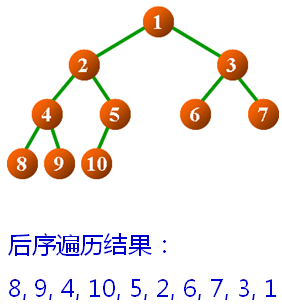
- 二叉树为空
- 无操作,直接返回
- 二叉树不为空
- 后序遍历左子树
- 后序遍历右子树
- 访问根结点中的数据元素
- 二叉树为空
-
后序遍历功能定义
postOrderTraversal(node){
if(node!=nullptr){
postOrderTraversal(node->left);
postOrderTraversal(node->right);
access(node->value);
}
} -
需要考虑的问题 是否可以将二叉树的典型遍历算法集成到BTree中?如果可以,代码需要做怎样的改动?
-
设计要点
- 不能与层次遍历函数冲突,必须设计新的函数接口
- 算法执行完成后,能够方便的获得遍历结果
- 遍历结果能够反映结点访问的先后次序
-
函数接口设计
SharedPointer<Array<T>> travrtsal(BTTraversal order)- 根据参数order选择执行遍历算法(先序,中序,后序)
- 返回值为堆中的数组对象(生命期由智能指针管理)
- 数组元素的次序反映遍历的先后次序
-
典型遍历示例
SharedPointer<Array<int>> sp = nullptr;
sp=tree.traversal(PreOrder);
for(int i=0;i<(*sp).length();i++){
cout<<(*sp)[i]<<endl;
}
编程实验
-
二叉树的典型遍历方式
小结
- 二叉树的典型遍历都是以递归方式执行的
- BTree以不同的函数接口支持典型遍历
- 层次遍历与典型遍历互不冲突
- 遍历结果能够反映树结点访问的先后次序
68 二叉树的比较于相加
二叉树的比较于相加(一)
-
二叉树的克隆操作
SharedPointer<BTree<T>> clone() const- 克隆当前树的一份拷贝
- 返回值为堆空间中的一棵新二叉树(与当前树相等)
-
二叉树的克隆
- 定义功能:clone(node)
- 拷贝node为根结点的二叉树(数据元素在对应位置相等)

- 定义功能:clone(node)
编程实验(一)
-
二叉树的克隆
二叉树的比较于相加(二)
-
二叉树比较操作的定义
- 判断两棵二叉树中的数据元素是否对应相等
bool operator==(const BTree<T> &btree)bool operator != (const BTree<T> &btree)
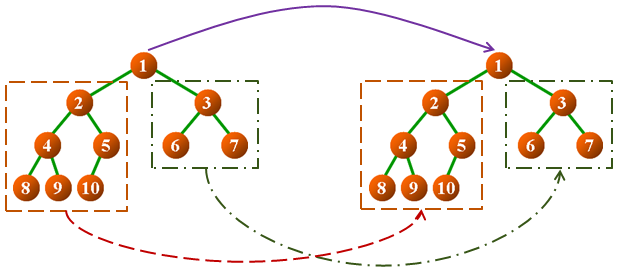
- 判断两棵二叉树中的数据元素是否对应相等
-
二叉树的比较
- 定义功能:equal(lh,rh)
- 判断lh为根结点的二叉树与rh为根结点的二叉树是否相等

编程实验(二)
-
二叉树的相等比较
二叉树的比较于相加(三)
-
二叉树的相加操作
SharedPointer<BTree<T>> add(const BTree<T> &btree)const- 将当前二叉树与参数btree中的数据元素在对应位置处相加
- 返回值(相加的结果)为堆空间中的一棵新二叉树
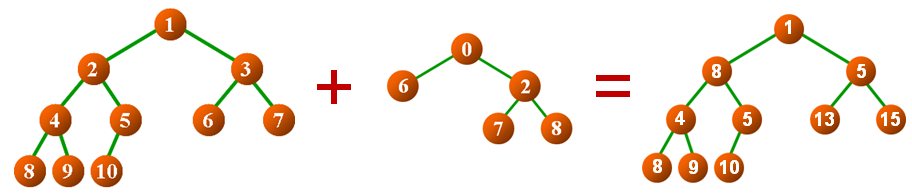
-
二叉树的加法
- 定义功能:add(lh,rh)
- 将lh为根结点的二叉树与rh为根结点的二叉树相加

- 定义功能:add(lh,rh)
编程实验(三)
-
二叉树的相加
小结
- 比较操作判断两棵二叉树中的数据元素是否对应相等
- 克隆操作将当前二叉树在堆空间进行复制
- 相加操作将两棵二叉树中的数据元素在对应位置处相加
- 相加操作的结果保存在堆空间的一棵二叉树中